西双版纳2024下半年事业单位笔试备考职测试题+答案（8月10日）(2)

　　1.【答案】B

　　【解析】第一步，本题考查容斥问题，属于二集合容斥类。

　　第二步，设两个系列都没用过的有x人，根据二集合容斥公式，有67+43-21=100-x，解得x=11。

　　因此，选择B选项。

　　2.【答案】B

　　【解析】第一步，本题考查容斥问题中的二集合容斥类，用公式法解题。

　　第二步，设两次测试中都合格的运动员有x人。

　　第三步，根据二集合容斥原理公式可列方程：50-17=26+21-x，解得：x=14。

　　因此，选择B选项。

　　3.【答案】D

　　【解析】第一步，本题考查容斥问题中的二集合容斥原理，用公式法解题。

　　第二步，设同时参加物理和数学两科竞赛的人数为x，根据二集合容斥原理的公式可列出：30+32-x=60-20，解得x=22。

　　因此，选择D选项。

　　4.【答案】D

　　【解析】第一步，本题考查容斥问题，属于二集合容斥类，用公式法解题。

　　第二步，选中A方案的人数为(人)，选B方案的人数为60+6=66(人)，设两个方案都喜欢的有3x人，都不喜欢的人数为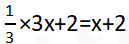(人)。根据二集合容斥公式，总数-都不满足的=集合A+集合B-都满足的，代入数据得：100-(x+2)=60+66-3x，解得x=14。

　　第三步，两个方案都不喜欢的人数为14+2=16(人)。

　　因此，选择D选项。

　　5.【答案】C

　　【解析】第一步，本题考查容斥问题，属于二集合容斥类，用公式法解题。

　　第二步，设总人数为20x，则懂法语的为15x人，懂英语的为16x人，两种都会的为13x人。代入二集合容斥公式：总数-都不满足的=集合A+集合B-都满足的，得到20x-10=15x+16x-13x，解得x=5，总人数为100人。

　　因此，选择C选项。

　　6.【答案】C

　　【解析】解法一：

　　第一步，本题考查容斥问题，属于二集合容斥类，用公式法解题。

　　第二步，设既是全运会又是奥运会志愿者的有x人，根据二集合公式，可得10+17-x=50-30，解得x=7。

　　第三步，则全运会志愿者中非奥运会志愿者的有17-7=10人。

　　因此，选择C选项。

　　解法二：

　　第一步，本题考查容斥问题，属于二集合容斥类，用画图法解题。

　　第二步，根据题目条件可画图如下：

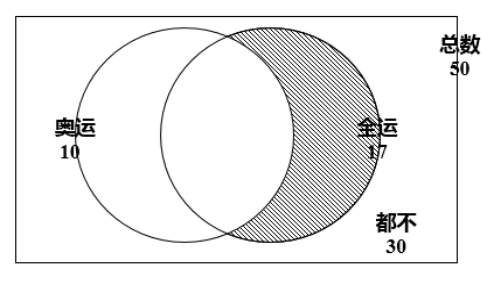
　　第三步，由图可知，班内是全运会志愿者而非奥运会志愿者的同学数(阴影部分)=50-30-10=10人。

　　因此，选择C选项。

　　【拓展】画图法在列式时，注意每部分数据只能加一遍且每部分都要涉及。

　　7.【答案】B

　　【解析】第一步，本题考查容斥问题，属于三集合容斥类，用公式法解题。

　　第二步，根据题意及“报名参加两个小组的48人”，可知本题为三集合非标准型容斥问题，设四年级共有x名学生，根据公式有：x-21=43+62+90-48-2×20，得x=128。

　　因此，选择B选项。

　　【拓展】三集合非标准型核心公式：总数-都不满足的=集合A+集合B+集合C-只满足两种的-2×都满足的

　　8.【答案】C

　　【解析】第一步，本题考查容斥问题，属于三集合容斥类，用公式法解题。

　　第二步，已知A∩B、B∩C和A∩C，符合三集合标准公式应用条件，即：总数-都不满足的=集合A+集合B+集合C-A∩B-B∩C-A∩C+都满足的。设三本书全读过的有x人，根据“至少读过其中一本的有20人”，可知都不满足的=0，代入数据，可得：20=10+12+15-8-9-7+x，解得x=7。

　　因此，选择C选项。

　　9.【答案】C

　　【解析】第一步，本题考查容斥问题，属于三集合容斥类。

　　第二步，设三样都有的x户，由三集合容斥标准型公式可得：100-5=30+66+88-17-56-22+x，解得x=6。

　　因此，选择C选项。

　　10.【答案】D

　　【解析】第一步，本题考查容斥问题，属于三集合容斥类，用方程法解题。

　　第二步，设参加两种兴趣夏令营的有x人，根据公式有：285+218+171-x-2×86=355，解得x=147(人)，说明355个人中，有147人参加了两种夏令营，86人参加了三种夏令营，则只参加了一种兴趣夏令营有355-147-86=122(人)。

　　因此，选择D选项。

（编辑：xufurong）